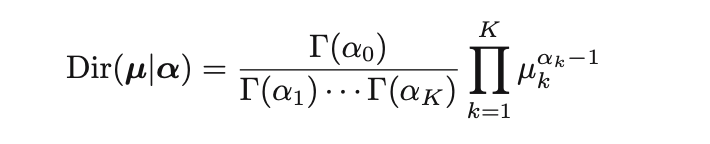
PRML chapter2

Posted on 2020-01-16 | In PRML | Visitors:

1.1

PRML chapter1

Posted on 2020-01-14 | In PRML | Visitors:

式1.57, 1.58

用MLE计算Gaussian分布的sample mean和sample variance。

首先log likelihood可以化简为： \[ \begin{align} \mathcal{L} = \ln P(x|\mu, \sigma^2) &= \sum\limits_{i=1}^{N}\ln \mathcal{N}(x|\mu, \sigma^2) \\ &= \sum\limits_{i=1}^{N}\ln \frac{1}{\sqrt{2\pi\sigma^2}} + \ln \exp(\frac{(x_i-\mu)^2}{-2\sigma^2}) \\ &= \sum\limits_{i=1}^{N} \frac{(x_i - \mu)^2}{-2\sigma^2} - \frac{N}{2} \ln2\pi - \frac{N}{2}\ln\sigma^2 \end{align}\ \] 先对$\mu$求偏导, 可以求得$\mu_{MLE}$： \[ \begin{align} \frac{\partial \mathcal{L}}{\partial \mu} &= \sum\limits_{i=1}^{N}\frac{x_i - \mu}{\sigma^2} = 0 \\ &\Leftrightarrow N\mu_{MLE} = \sum\limits_{i=1}^{N}x_i \\ &\Leftrightarrow \mu_{MLE} = \frac{1}{N}\sum\limits_{i=1}^{N}x_i \end{align} \] 同时我们可以验证我们的sample mean和数据源自的Gaussian分布的真正均值$\mu$是相等的： \[ \begin{align} \mathbb{E}[\mu_{MLE}] &= \frac{1}{N}\mathbb{E}[\sum\limits_{i=1}^{N}x_i] = \mu \end{align} \] 再来算 $\sigma^2_{MLE}$: \[ \begin{align} \frac{\partial \mathcal{L}}{\partial \sigma^2} &= \sum\limits_{i=1}^{N}\frac{\partial\frac{(x_i-\mu)^2}{-2\sigma^2}}{\partial\sigma^2} - \frac{\partial\frac{N}{2}\ln \sigma^2}{\partial\sigma^2} \\ &= \frac{\sum\limits_{i=1}^{N}(x_i-\mu)^2}{2} \frac{1}{\sigma^4} - \frac{N}{2\sigma^2} = 0 \\ \end{align} \] 左右同乘 $2\sigma^4$, 代入 $\mu_{MLE}$ 整理可以得出： \[ \sigma^2_{MLE} = \frac{1}{N}\sum\limits_{i=1}^{N}(x_i - \mu_{MLE})^2 \] 需要注意的是通过极大似然估计出来的 $\sigma^2_{MLE}$ 会低估实际分布的方差，所以是一个有偏估计(过拟合问题也与此相关)： \[ \begin{align} \mathbb{E}[\sigma^2_{MLE}] &= \mathbb{E}[\frac{1}{N}\sum\limits_{i=1}^{N}(x_i - \mu_{MLE})^2] \\ &= \frac{1}{N}\sum\limits_{i=1}^{N}\mathbb{E}[(x_i^2 + \mu_{MLE}^2 - 2x_i\mu_{MLE})] \\ &= \frac{1}{N}\sum\limits_{i=1}^{N}(\mathbb{E[x_i^2]} + \mathbb{E}[\mu_{MLE}^2] - 2\mu_{MLE}\mathbb{E}[x_i]) \\ &= \frac{1}{N}\sum\limits_{i=1}^{N}(\mathbb{E[x_i^2]} - \mathbb{E}[\mu_{MLE}^2]) \\ &= \mathbb{E}[\frac{1}{N}\sum\limits_{i=1}^{N}(x_i^2 - \mu^2)] - \mathbb{E}[\mu_{MLE}^2 - \mu^2] \\ &= \frac{1}{N}\sum\limits_{i=1}^{N} \mathrm{Var}(x_i) - [\mathbb{E}[\mu_{MLE}^2] - \mathbb{E}[\mu^2]] \\ &= \frac{1}{N}\sum\limits_{i=1}^{N} \mathrm{Var}(x_i) - \mathrm{Var}(\mu_{MLE}) \\ &= \sigma^2 - \mathrm{Var}(\frac{1}{N}\sum\limits_{i=1}^{N}x_i) \\ &= \frac{N-1}{N}\sigma^2 \end{align} \]

式1.67

从MAP角度来看curve fitting problem。

我们先假定曲线的权重 $w$ 符合Gaussian分布的先验: \[ P(w|\alpha) = \mathcal{N}(w|0, \alpha^{-1}I) = (\frac{\alpha}{2\pi})^{(M+1)/2}\exp (-\frac{\alpha}{2}w^Tw) \] 则我们知道后验概率正比于似然函数与先验分布的乘积： \[ P(w|x,t,\alpha,\beta) \propto P(t|x,\alpha,\beta)P(w|\alpha) \] 于是最大化后验概率就变成了最大化 $P(t|x,\alpha,\beta)P(w|\alpha)$： \[ \begin{align} \ln P(t|x,\alpha,\beta)P(w|\alpha) &= \ln P(t|x,\alpha,\beta) + \ln P(w|\alpha) \\ \end{align} \] 我们分开看这两项： \[ \ln P(t|x,\alpha,\beta) = -\frac{\beta}{2}\sum\limits_{n=1}^{N}\{y(x_n, w) - t_n\}^2 + \frac{N}{2}\ln \beta - \frac{N}{2} \ln (2\pi) \]

\[ \begin{align} \ln P(w|\alpha) &= \ln (\frac{\alpha}{2\pi})^{(M+1)/2} + (-\frac{\alpha}{2}w^Tw)\\ &= -\frac{\alpha}{2}w^Tw + \frac{M+1}{2}\ln (\frac{\alpha}{2\pi}) \end{align} \]

最大化 $\ln P(t|x,\alpha,\beta) + \ln P(w|\alpha)$ 相当于最大化 $-\frac{\alpha}{2}w^Tw - \frac{\beta}{2}\sum\limits_{n=1}^{N}\{y(x_n, w) - t_n\}^2$, 也就是最小化 $\frac{\alpha}{2}w^Tw + \frac{\beta}{2}\sum\limits_{n=1}^{N}\{y(x_n, w) - t_n\}^2$ (前一项是正则项，后一项是error function), 也就是说当权重的先验是Gaussian分布的时候MAP和岭回归(Ridge Regression)等价。

transformation of random variables

Posted on 2020-01-13 | In PRML | Visitors:

The goal is to find the distribution of the transformed random variable or joint distribution

of the random vector.

Theorem 8.1.1 (Change of variables in one dimension). Let X be a continuous r.v. with PDF $f_X$, and let Y = g(X), where g is differentiable and strictly increasing (or strictly decreasing). Then the PDF of Y is given by: \[ f_Y(y) = f_X(x)\left| \dfrac{dx}{dy} \right|\\ \] proof: \[ \begin{align} F_Y(y) &= P(Y ≤ y)\\ &= P(g(X) ≤ y) \\ &= P(X ≤ g^{-1}(y)) \\ &= F_X(g^{-1}(y)) \\ &= F_X(x) && (y = g(x)) \\ \end{align} \]

So we can have the formula: $f_Y(y) = \dfrac{dF_Y(y)}{dy} = \dfrac{dF_X(x)}{dy} = \dfrac{dF_X(x)}{dx}\dfrac{dx}{dy} = f_X(x)\left| \dfrac{dx}{dy} \right|$

Theorem 8.1.5 (Change of variables). Let X = (X1, . . . ,Xn) be a continuous random vector with joint PDF X, and let Y = g(X) where g is an invertible function from $R^n$ to $R^n$. (The domain of g does not actually have to be all of $R^n,$ but it does need to be large enough to contain the support of X, else g(X) could be undefined!) \[ \begin{align} f_Y(y) = f_X(x)\left|\dfrac{\partial x}{\partial y}\right| \end{align} \] The $\dfrac{\partial x}{\partial y}$ is the Jacobian matrix.

The Box-Muller example: Let U ~ Unif(0, $2\pi$), and let T ~ Exp(1) be independent of U. Define X = $\sqrt{2T}cosU$ and Y = $\sqrt{2T}sinU$. Find the joint PDF of (X, Y ). Are they independent? What are their marginal distributions? \[ \begin{align} f_{X,Y}(x, y) &= f_{T,U}(t,u) \left| \begin{array}{cc} \frac{\partial t}{\partial x} & \frac{\partial t}{\partial y} \\ \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \end{array} \right|\\ &= 1 \cdot e^{-t} \frac{1}{2\pi} \cdot 1 \\ &= \frac{e^{\frac{x^2 + y^2}{-2}}}{2\pi} \\ &= \frac{1}{\sqrt{2\pi}}e^{\frac{x^2}{-2}} \cdot \frac{1}{\sqrt{2\pi}}e^{\frac{y^2}{-2}} \end{align} \]

明天太阳照常升起的概率

Posted on 2020-01-10 | In PRML | Visitors:

结合PRML和shuhuai008大哥的讲解重新理解拉普拉斯太阳照常升起的问题

问题：太阳已经照常升起N天了，明天太阳照常升起的概率是多少？

$X: $ 事件that太阳已经照常升起了N天

$Y: $ 事件that太阳明天会照常升起

$\theta :$ 对于任意一天而言，太阳照常升起的概率，在区间$[0, 1]$上， $P(\theta) = 1$(均匀分布的概率密度函数)

一个粗浅的视角

step 1: 贝叶斯估计 \[ \begin{align} P(\theta|X) &= \dfrac{P(X|\theta)P(\theta)}{\int_0^1 P(X|\theta)P(\theta)d\theta} \\ &= \dfrac{P(X|\theta)}{\int_0^1 P(X|\theta)d\theta} \\ &= \dfrac{\theta^N}{\int_0^1 \theta^N d\theta} \\ &= \dfrac{\theta^N}{\frac{1}{N+1}\theta^{N+1}|_0^1} \\ &= \dfrac{\theta^N}{\frac{1}{N+1}} \\ &= (N+1)\theta^N \end{align} \] step 2: 贝叶斯预测 \[ \begin{align} P(Y|X) &= \int_0^1 P(Y|X,\theta) d\theta \\ &= \int_0^1 P(Y|\theta) P(\theta|X) d\theta \\ &= \int_0^1 \theta (N+1)\theta^N d\theta \\ &= (N+1)\int_0^1 \theta^{N+1} d\theta \\ &= \dfrac{N+1}{N+2} \end{align} \]

一个没那么粗浅的视角

我们一样给 $\theta$ 一个先验Beta(a, b)，使用Beta分布作为参数的先验的好处在于Beta分布是二项的一个共轭先验，我们可以得到： \[ P(\theta|m ,l, a, b) = \frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)} \theta^{m+a-1}(1-\theta)^{l+b-1} \] 我们想要的明天太阳照常升起的概率为： \[ P(x=1|X) = \int_{0}^{1}P(x=1|\theta)P(\theta|X)d\theta = \int_{0}^1\theta P(\theta|X)d\theta = \mathbb{E}_\theta[\theta|X] \] 由于共轭性质， $\theta|X$也是一个Beta分布，其均值为 $\dfrac{m+a}{m+a+l+b}$。

在我们的问题中，$m = N$ , $l = 0$，同时对于 $\theta$的先验是一个[0, 1]上的均匀分布，所以 $a = b = 1$，于是最终的结果为： \[ P(x=1|X) = \dfrac{N+1}{N+2} \]

Rvalue reference and their use

Posted on 2019-04-06 | In C++ | Visitors:

这是Laurent Kneip教授的CS133的第7讲，上课的时候听的迷迷糊糊的，但是后来写作业的时候觉得这些内容非常重要但是不容易理解，所以写一点总结。

motivation

我们想要让一个class来代替programmer来管理动态分配的memory，在constructor里面分配资源，在deconstructor里面de-allocate.

Smart pointer:

template <class T>
  class Auto_ptr1 {
    T* m_ptr;
    public:
    Auto_ptr1(T* ptr=nullptr) : m_ptr(ptr) {}
    ~Auto_ptr1() {delete m_ptr;}
    
    // overload deference and operator ->
    // let us use Auto_ptr like m_ptr
    T& operator*() const {return *m_ptr;}
    T* operator->() const {return m_ptr;}
  }

现在我们就可以愉快地用Smart pointer了，比如：

void function() {
  Auto_ptr<Resource> ptr(new Resource);
  int x = somevalue;
  if (x == 0) {
    return; // 不必担心内存泄漏
  } else {
    ptr->sayHi();
  }
}

Auto-pointer flaw

int main() {
  Auto_ptr1<Resource> res1(new Resource);
  Auto_ptr1<Resource> res2(res1); // both res1 and res2 are pointing to
  																// at the same resource
  
  return 0;
}
or
int main() {
  Auto_ptr1<Resource> res1(new Resource);
  Auto_ptr1<Resource> res2;
  res2 = res1;
  
  return 0;
}
// Resource acquired
// Resource destroyed
// Segmentation fault

solutions to the Auto_ptr flaw

solution 1: prevent the copy constructor and assignment operator to be "available"

method 1: explicitly declare copy constructor and make them private

template <class T>
  class Auto_ptr1 {
    T* m_ptr;
    public:
    Auto_ptr1(T* ptr=nullptr) : m_ptr(ptr) {}
    ~Auto_ptr1() {delete m_ptr;}
    // ...
		private:
    Auto_ptr(const Auto_ptr1 &);
    Auto_ptr& operator= (const Auto_ptr1 &);
  }

problem: less efficient than the default constructor, member functions and friends can still call the private defined constructors, unclear

method 2: the C++11 way

template <class T>
  class Auto_ptr1 {
    T* m_ptr;
    public:
    Auto_ptr1(T* ptr=nullptr) : m_ptr(ptr) {}
    ~Auto_ptr1() {delete m_ptr;}
    // ...
    Auto_ptr(const Auto_ptr1 &) = delete;
    Auto_ptr& operator= (const Auto_ptr1 &) = delete;
  }

pass by value is no longer available -> we can just pass reference

however, we can no longer do this:

??? generateResource() {
  Resource *r = new Resource;
  return Auto_ptr1(r);
}
// can't return by reference because object will be destroyed
// can't return by value because copy-constructor is disabled

move semantics

我们不想copy value, just move ownership

template <class T>
  class Auto_ptr2 {
    T* m_ptr;
    public:
    Auto_ptr2(T* ptr=nullptr) : m_ptr(ptr) {}
    ~Auto_ptr2() {delete m_ptr;}
    // ...
    T& operator*() const {return *m_ptr;}
    T* operator->() const {return m_ptr;}
    bool isNull() const {return m_ptr == nullptr;}
    
    // something new here
    // copy constructor with move semantics
    Auto_ptr2(Auto_ptr2 &a) { // no longer const
      m_ptr = a.ptr;
      a.ptr = nullptr;
    }
    Auto_ptr2& operator= (Auto_ptr2 &a) {
      if (&a == this) return *this;
      delete m_ptr;
      m_ptr = a.m_ptr;
      a.m_ptr = nullptr;
      return *this;
    }
  }

std::auto_ptr is implemented exactly like this in original C++98 standard
problem occurs if pass by value
removed since C++17

Lvalues and Rvalues

general rule: if you can take its address, it's an lvalue, else, it's an rvalue

some examples:

template<typename T1, typename T2>
int sizeDiff(const T1 &c1, const T2 &c2) {
	return c1.size() - c2.size();
}

lvalue: sizeDiff, c1, c2

rvalue: return value

int *px;
std::vector<int> v;
std::unordered_set<int> s;
...
*px = sizeDiff(v, s);

lvalue: px, v, s

rvalue: sizeDiff(v, s)

1	std::ifstream myinput(std::string("something"));

anonymous objects are rvalues

Rvalues die at the end of an expression
- they can't be assigned to

but there is a special case:

void printSomething(const std::string &str) {
  // the parameter is an lvalue(object with name and space)
  std::cout << str << std::endl;
}
int main() {
  printSomething(std::string("hello")); // we passed in an rvalue!!!
  return 0;
}

local const reference can be used to prolong the lifetime of temporary value and refers to it until the end of the containing scope(does not incur the cost of a copy-construction)

Rvalue references

1
2
3

int x = 5;
int &lref = x; // lvalue reference initialized with lvalue x
int &&rref = 5; // rvalue reference initialized with rvalue 5

rvalue reference allows us to
- extend the lifespan of the (rvalue) object by the lifespan of the rvalue reference
- modify the rvalue

move construction and move assignment

template<class T>
  class Auto_ptr3 {
    T* m_ptr;
    public:
    Auto_ptr3(T* ptr=nullptr) : m_ptr(ptr) {}
    ~Auto_ptr3() {delete m_ptr;}
    
    // copy constructor: do deep copy of a.m_ptr to m_ptr
    Auto_ptr3(const Auto_ptr3 &a) {
      m_ptr = new T;
      *m_ptr = *a.m_ptr;
    }
    // copy assignment: do deep copy of a.m_ptr to m_ptr
    Auto_ptr3& operator=(const Auto_ptr3& a) {
      if (&a == this) return *this;
      
      delete m_ptr;
      m_ptr = new T;
      *m_ptr = *a.m_ptr;
      return *this;
    }
    
    T& operator*() const {return *m_ptr;}
    T* operator->() const {return m_ptr;}
    bool isNull() const {return m_ptr == nullptr;}
  };

the usage:

class Resource {
  public:
  Resource() {std::cout << "resource acquired\n";}
  ~Resource() {std::cout << "resource destroyed\n";}
};
Auto_ptr3<Resource> generateResource() {
  Auto_ptr3<Resource> res(new Resource);
  return res; // return value invokes copy constructor
}
int main() {
  Auto_ptr3<Resource> mainres; // no output until now
  mainres = generateResource(); // generateResource() print 1, copy assignment print 1
  return 0;
}

output:

resource acquired
resource acquired
resource destroyed
resource destroyed

2 allocations to create an object, inefficient but very safe

move construction/assignment
- role: move ownership from one obj to another
- use instead of copying to gain efficiency
- similar to regular copy constructor/assignment oprator
  - take non-const rvalue reference instead of const lvalue reference

template<class T>
  class Auto_ptr4 {
    T* m_ptr;
    public:
    Auto_ptr4(T* ptr=nullptr) : m_ptr(ptr) {}
    ~Auto_ptr4() {delete m_ptr;}
    
    // copy constructor: do deep copy of a.m_ptr to m_ptr
    Auto_ptr3(const Auto_ptr3 &a) {
      m_ptr = new T;
      *m_ptr = *a.m_ptr;
    }
    // copy assignment: do deep copy of a.m_ptr to m_ptr
    Auto_ptr3& operator=(const Auto_ptr3& a) {
      if (&a == this) return *this;
      delete m_ptr;
      m_ptr = new T;
      *m_ptr = *a.m_ptr;
      return *this;
    }
    // move constructor: transfer ownership of a.m_ptr to m_ptr
    Auto_ptr4(Auto_ptr&& a) : m_ptr(a.m_ptr) {
      a.m_ptr = nullptr;
      // remove ownership
      // prevent a from destroying resource
      // prevent a from causing dangling pointers
    }
    // move assignment operator: transfer ownership of a.m_ptr to m_ptr
    Auto_ptr4& operator=(Auto_ptr4&& a) {
      // self-assignment detection
      if (&a == this) return *this;
      
      delete m_ptr;
      m_ptr = a.m_ptr;
      a.m_ptr = nullptr; // remove ownership, prevent a from destroying resource, prevent a from causing dangling pointers
      return *this;
    }

      
      
    T& operator*() const {return *m_ptr;}
    T* operator->() const {return m_ptr;}
    bool isNull() const {return m_ptr == nullptr;}
  };

and now we run the program again:

class Resource {
  public:
  Resource() {std::cout << "resource acquired\n";}
  ~Resource() {std::cout << "resource destroyed\n";}
};
Auto_ptr3<Resource> generateResource() {
  Auto_ptr3<Resource> res(new Resource);
  return res; // return value invokes copy constructor
}
int main() {
  Auto_ptr3<Resource> mainres; // no output until now
  mainres = generateResource(); // generateResource() print 1, copy assignment print 1
  return 0;
}

output:

1 2	resource acquired resource destroyed

key insights
- if an lvalue is used, like: a = b(we should make a deep copy and not alter b)
- if an rvalue is used, like: a = b + c(rvalue is about to be destroyed, it is reasonale to steal the ownership and avoid copying)

std::move

extension of move semantics to lvalues!

template<class T>
void swap(T& a, T& b) {
  T tmp{a}; // invokes copy constructor
  a = b; // invokes copy assignment
  b = tmp; // invokes copy assignment
}

however doing 3 copies is unnecessary, we can do 3 moves instead

solution: cast the lvalues to rvalues with std::move()

template<class T>
void swap(T& a, T& b) {
  T tmp {std::move(a)}; // invokes move constructor
  a = std::move(b); // invokes move assignment
  b = std::move(tmp); // invokes move assignment
}

what happens to the lvalue !?

一个小实验：

#include <iostream>
#include <vector>
#include <string>
using namespace std;

int main() {
	vector<string> vec;
	string str = "Knock";
	cout << "copying str\n";

	vec.push_back(str);
	cout << "str is:" << str << "and vec[0] is:" << vec[0] << endl;

	cout << "move str\n";

	vec.push_back(std::move(str));
	cout << "str is:" << str << "vec[0] is:" << vec[0] << "vec[1] is:" << vec[1] << endl;

	return 0;
}

output:

copying str
str is:Knockand vec[0] is:Knock
move str
str is:vec[0] is:Knockvec[1] is:Knock

objects that are being stolen from need to be left in a defined "null state"
they are not a temporary after all, and can be used again later

新东方B王讲托福口语

Posted on 2019-03-19 | In other | Visitors:

前几天来了个新东方的老师来学校讲托福口语怎么上23分，此人据说托福口语满分，那是相当厉害。简单地记了一下笔记，主要是在听他吹牛说相声。 #### 题型

task 1/2: agree or disagree
task 3_6: with materials（转述）

评分标准

Delivery 传达效果/直观性
- 模仿跟读
- 训练过程中对连贯性要近乎苛刻的要求
Language use
- 听自己的录音：找错、纠错、归档、重录
- 背文章：范例回答、新概念
Topic Development
- 刷题、TPO从后往前(TPO只做综合题，独立题做机经和)：www.superlearn.com
基本任务：音量（必须够）、口齿清晰
核心任务：表达流畅，语速（不能卡壳，you know… i mean...）
- 连贯性最重要，发现语法错误不要self correction
进阶任务：发音地道不需要过于关心
- 用词从简、生活化：保证了语言的连贯性
- 话题发展：
  - 内容：细节为主
  - 逻辑：宏观直线，观点从大到小

git使用方法

Posted on 2019-03-19 | In other | Visitors:

都已经是大三的人了，但是对git的用法还不是很熟悉，于是看了看廖雪峰的小站。虽然看完了之后还是没记住。

版本控制：分布式 VS 集中式

分布式安全
分布式不必联网
分布式有分支管理

创建版本库

git init
.git目录：跟踪管理版本库的
git add
git commit

时光机穿梭

git status：查看仓库当前状态
git diff：查看修改内容

版本回退

git commit相当于保存一个快照，游戏存盘
git log：查看commit的历史记录
git用HEAD表示当前版本，上个版本HEAD^{，上上个是HEAD}^，前100个是HEAD~100
git reset --hard HEAD^
git reflog：查看命令历史以便确定要回到未来的哪个版本

工作区与暂存区

工作区（working directory）
- 即init的文件夹
版本库：.git文件夹（repository）
- 版本库中有一个暂存区（stage）
- git add：工作区->stage， git commit：stage->分支

关于修改

每次修改，如果不add到stage里就不会被加入到commit
git checkout -- readme.txt可以丢弃工作区的修改，有两种情况
- 一种是readme.txt自修改后还没有被放到暂存区，现在，撤销修改就回到和版本库(原始的repository)一模一样的状态
- 一种是readme.txt已经添加到暂存区后，又作了修改，现在，撤销修改就回到添加到暂存区后的状态
- git checkout -- file命令中的--很重要，没有--，就变成了“切换到另一个分支”的命令
用命令git reset HEAD <file>可以把暂存区的修改撤销掉（unstage），重新放回工作区
总结：
- 场景1：当你改乱了工作区某个文件的内容，想直接丢弃工作区的修改时，用命令git checkout -- file。
- 场景2：当你不但改乱了工作区某个文件的内容，还添加到了暂存区时，想丢弃修改，分两步，第一步用命令git reset HEAD <file>，就回到了场景1，第二步按场景1操作。
- 场景3：已经提交了不合适的修改到版本库时，想要撤销本次提交，进行版本回退，不过前提是没有推送到远程库。

删除文件

假设file已经存在于repository里了
1. rm file（在工作区删除file）
2. git rm file
3. git commit -m "blabla"
如果将工作区的文件误删了，git checkout -- file
- git checkout其实是用版本库里的版本替换工作区的版本，无论工作区是修改还是删除，都可以“一键还原”。